2005-05-25
§ 距離が遠くても天体の見かけの大きさがそれほど変化しない理由
※下記の内容は、誤りを含んでいる可能性があります。以下のエントリを参照してください。
http://d.hatena.ne.jp/isana/20050615/p1
少し前に、マツドサイエンティスト・研究日誌の『遠近法が通用しない!?』というエントリが話題になっていました。
遠くに行けば行くほど小さく見えるのは、50億光年位までで、それ以上遠くなっても、物は小さく見えなくなる
えええええ!マジですか!宇宙の曲率?後退速度の相対論的効果?
と、かく言う私も目ン玉が飛び出るぐらいびっくりしたんだけど...
でも、よーく考えてみると、天体の見かけのサイズは距離に反比例しますよね。
反比例のグラフはもともとこういう形をしているんじゃないでしょうか。
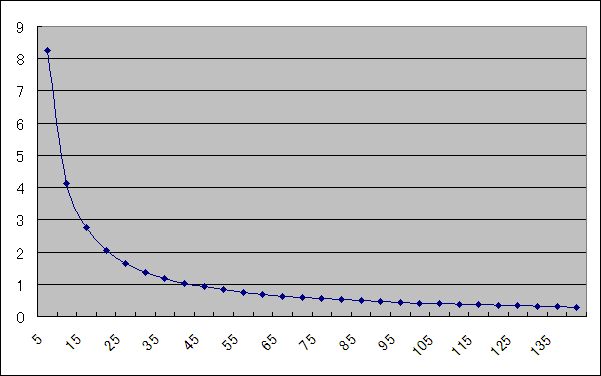
これは、直径10万光年の天体*1の見かけのサイズを以下の式で計算したもの。
θ = atan ( r / d ) * 2
縦軸が見かけのサイズ(秒角)、横軸が距離(億光年)。
*1 ちょうど銀河系と同じぐらい
つまり、これは「ある程度の距離になると、それ以上距離が広がっても視線角度はほとんど変化しない」というごく当たり前の遠近法では?
じつは、ここ数日、宇宙論的赤方偏移の値が「距離による空間の歪曲の率」を表すことに気づいて、おぉ!これであの「遠くのものが小さくならない現象」が計算で導けるのでは、とExcelを弄り回していたのです。
で、勢い込んでグラフにしてみたら、偏移はグラフの形にはほとんど影響しない。そりゃそうだよ、赤方偏移と距離は比例するんだからその分を上乗せしてもグラフの形は変わらない。
そこで初めて、「遠くのものは小さく見えるけど、決して見えなくなることはない」という当たり前の事実に気づいたのでした。*1。
*1 嘘だと思ったら、外に出て等間隔に並んでいる電柱かなにかで確かめてみてください
ちなみに、宇宙論的な空間の歪曲を考慮した(と思われる)「天体の見かけのサイズのグラフ」は以下のとおり。
http://www.lizard-tail.com/isana/tmp/virtual_height2.jpg
§ [book] 松浦晋也『恐るべき旅路 ―火星探査機「のぞみ」のたどった12年―』(amazon)
傑作。一機の探査機が計画され、紆余曲折を経て設計・製作に至り、打上げのときを迎え、軌道上で思わぬトラブルに見舞われ、それでもなおエンジニアの懸命の努力によって延命し、最後の最後、あと一歩というところで目標の軌道への投入に失敗、プロジェクトの断念が決定される。そのプロセスを克明に追ったルポ。
読後、震えるような感動を覚えた。
ひたすら地道な取材と調査、そしてなにより当事者の言葉を丁寧に丁寧に拾いながら、この極めて複雑で長期にわたるプロジェクトの全貌を描き出した作者の努力と力量には、ただただ頭が下がる。
日本のノンフィクション史に残る傑作だと思う。いや、まじで。